概括

特点

粒子群算法具有收敛速度快、参数少、算法简单容易实现的优点，但是会有局部最优解的情况发生。

基本思路

粒子群算法主要模拟鸟类觅食的行为，所以我们设想我们的“小鸟”在森林中随机搜索，每一只”小鸟“都向着自己判断的方向搜索，并记录搜索过程中食物最多的位置，同时进行共享，这样“小鸟”们就知道哪个为止的食物最多。在整个搜索过程中每只“小鸟”都会根据鸟群当前的信息来调整自己的搜索策略。

基本原理

6个重要参数

粒子位置 $X_{i d}$
粒子速度 $V_{i d}$
第i个粒子搜索到的最优位置 $P_{i, p b e s t}$
群体搜索的最优为止 $P_{d, g b e s t}$
第i个例子搜索到的最优位置的优化目标函数值 $f_{p}$
群体搜索的最优位置的优化目标函数值 $f_{g}$

流程图

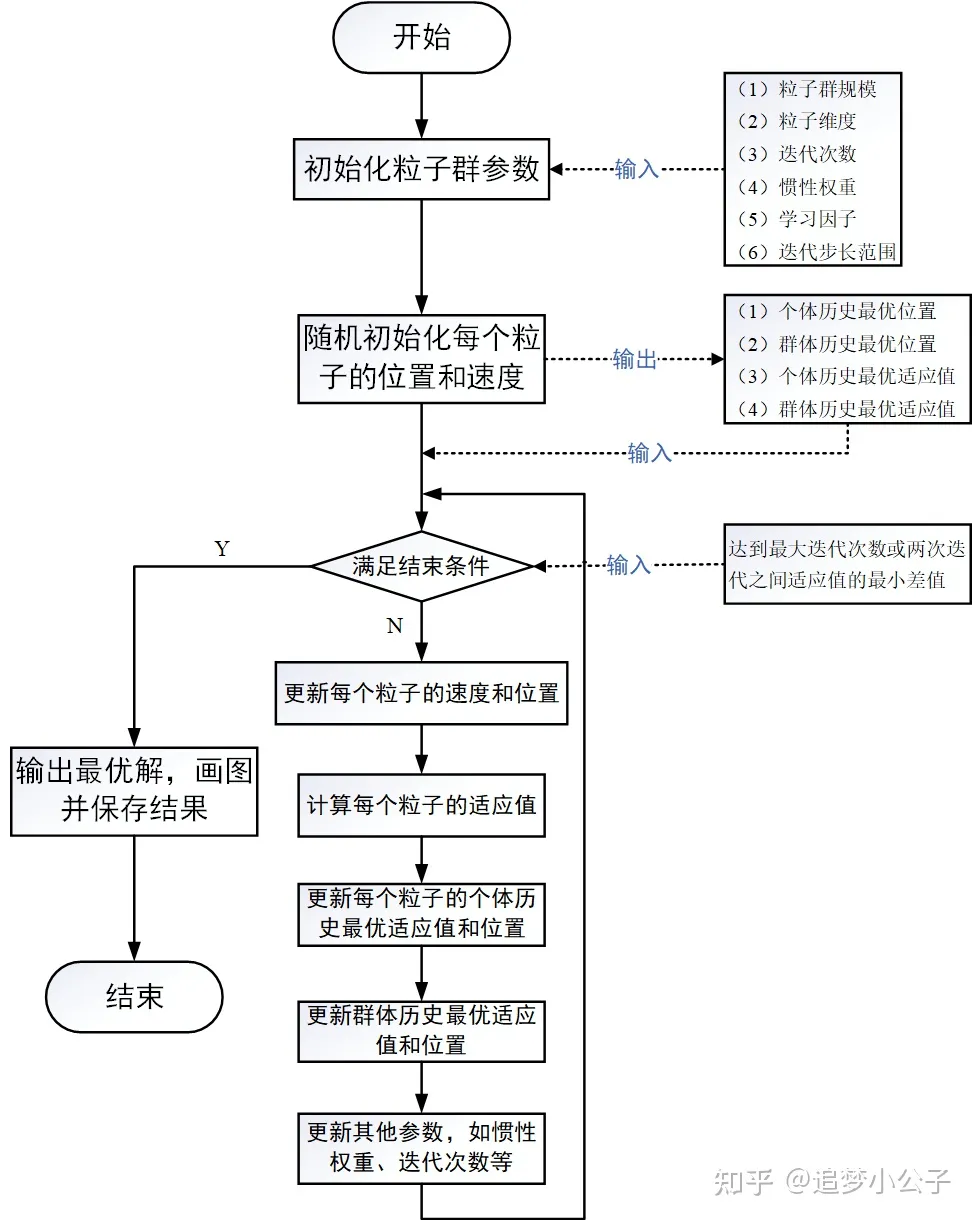
参数详解

粒子群规模：N

没啥好说的，越多越好，但是随着数量的增加，“性价比”会很低。

粒子维度：D

根据优化目标函数的自变量个数进行设置。

迭代次数：K

字面意思，特点和粒子群规模差不多。

（经典取值：60、70、100）

惯性权重： $ω$

动态调整惯性权重以平衡收敛的全局性以及收敛速度。

含义

表示上一代粒子的速度对当代粒子速度的影响。 $ω$ 越大，探索新区域的能力越强，全局搜索能力越大（受群体影响小），但是局部寻优能力弱。所以，我们希望 $ω$ 不是一个定值，而是前期大后期小，在前期提高全局搜索能力，在后期提高局部搜索能力时期提升收敛速度。

特别的，当 $ω$ =1时，退化为基本粒子群算法，当 $ω$ =0时，粒子失去对本身经验的思考。

推荐取值：0.9、1.2、1.5、1.8

改善 $ω$

从上文可以得知我们希望 $ω$ 不是一个定值，所以我们采用一种常用的自适应调整策略——线性变化策略：在每次迭代过程中线性地减少 $ω$ :

ω = ω_{m a x} - (ω_{m a x} - ω_{m i n}) \frac{i t e r}{i t e r_{m a x}}

学习因子： $c_{1}, c_{2}$

也称作加速系数或者加速因子。

$c1 $表示粒子下一步动作中自身经验部分的占比，指将粒子推向个体最优位置$ P{id,pbest}$的加速权重；
$c2 $表示粒子下一步动作来源于其他粒子经验部分的占比，指将粒子推向群体最优位置$ P^k{d,gbest}$的加速权重；
$c_{1}$ =0时称为无私型粒子群算法，容易陷入局部最优解；
$c_{2}$ =0时称为自我认识粒子群算法，没有信息共享，会导致算法收敛慢甚至无法收敛；
$c_{1} \times c_{2} \neq 0$ 时称之为完全粒子群算法，一般最优。

经典取值： $c_{1} = c_{2} = 2$ 、 $c_{1} = 1.6 ， c_{2} = 1.8$ 、 $c_{1} = 1.6 ， c_{2} = 2$

速度更新公式

（都是向量）

v_{i d}^{k + 1} = ω v_{i d}^{k} + c_{1} r_{1} (p_{i d, p b e s t}^{k} - x_{i d}^{k}) + c_{2} r_{2} (p_{d, g b e s t}^{k} - x_{i d}^{k})

1.速度公式解释

第一项：惯性部分
第二项：认知部分
第三项：社会部份

2.参数定义

$N$ ——粒子群规模； $i$ ——粒子序号；

$D$ ——粒子维度； $d$ ——粒子维度序号；

$k$ ——迭代次数； $ω$ ——惯性系数； $c_{1}$ ——个体学习因子； $c_{2}$ ——群体学习因子；

$r_{1}, r_{2}$ ——区间[0,1]内的随机数，增加搜索随机性；

$v_{i d}^{k}$ ——粒子i在第k次迭代中在第d维的速度向量；

$x_{i d}^{k}$ ——粒子i在第k次迭代中在第d维的位置向量；

$p_{i d, p b e s t}^{k}$ ——粒子i在第k次迭代中第d维的历史最优位置，即在第k次迭代后，第i个粒子得到的最优解；

$p_{i d, g b e s t}^{k}$ ——群体在第k次迭代中第d维的历史最优为止，即在第k次迭代后，整个例子群体中的最优解。

位置更新公式

x_{i d}^{k + 1} = x_{i d}^{k} + v_{i d}^{k + 1}

matlab代码（二维）

matlab

clear 
clc

%绘制原图        图1目标函数的三维网格图
x1=-15:0.1:15
x2=-15:0.1:15;
[x1,x2]=meshgrid(x1,x2);

y=(x1.^2)/3+(x2.^2)/4;
mesh(x1,x2,y);    
hold on;

%%预设参数
n=300; %粒子群的规模
d=2; %变量个数
c1=2;
c2=2;
w_max=1;
w_min=0.1;
w=0;
K=300; %迭代次数

%%分布粒子的取值范围及速度的取值范围
x=-10+20*rand(n,d);  %x在[-10,10]中取值
v=-5+10*rand(n,d); %v在[-5,5]中取值

%%计算适应度
fit=zeros(n,1);
for j=1:n
    fit(j)=A11_01(x(j,:));
end
pbest=x;%个人最优点即为初始点
ind=find(min(fit)==fit);% 找最小值
gbest=x(ind,:);%群体最优点
h=scatter3(x(:,1),x(:,2),fit,'o');  %图2 粒子的初始分布图

%%更新速度与位置
for i=1:K%迭代
    for m=1:n%按维度更新
       w=w_max-(w_max-w_min)*(i/K);
       v(m,:)=w*v(m,:) + c1*rand*(pbest(m,:)-x(m,:)) + c2*rand*(gbest-x(m,:));%rand是[0,1]随机数
       %限制速度
       v(m,find(v(m,:)<-5))=-5;%这里发现速度小于-5时取-5
       v(m,find(v(m,:)>5))=5;%这里发现速度大于5时取5
       
       x(m,:)=x(m,:)+v(m,:);%位置更新

       %限制位置
       x(m,find(x(m,:)<-10))=-10;%这里发现位置小于-10时取-10
       x(m,find(x(m,:)>10))=10;%这里发现位置大于10时取10
       
       %重新计算适应度
       fit(m)=A11_01(x(m,:));
       if x(m,:)<A11_01(pbest(m,:))
           pbest(m,:)=x(m,:);
       end
       if A11_01(pbest(m,:))<A11_01(gbest)%小
           gbest=pbest(m,:);
       end
    end
    fitnessbest(i)=A11_01(gbest);%最优点  
    pause(0.01);    %为了直观，每更新一次，暂停0.01秒
    h.XData=x(:,1);
    h.YData=x(:,2);
    h.ZData=fit;
end
hold off;
plot(fitnessbest);
xlabel('迭代次数');
function y=A11_01(x)
    y=x(1)^2/3+x(2)^2/4;
end

我们需要重点考虑的问题

1.适应值

就是优化目标函数的值。

2.位置限制

自变量范围，就是定义域。

3.速度限制

跑太快会错过最优解。

$v_{m a x}$ 一般设置为例子变化范围的10%~20%.

4.优化停止准测

达到最大迭代步数
达到满意解

5.初始化

粒子群算法优化的结果受很多因素的影响，其中受粒子初始值的影响比较大，而且较难调控。如果粒子初始值是随机初始化的，在不改变任何参数的情况下，多次优化的结果不一定都收敛到一个全局或局部最优解，也可能会得到一个无效解。所以粒子初始化是一个十分重要的步骤，它关系到整个优化过程中优化收敛的速度与方向。如果粒子的初始化范围选择得好的话可以大大缩短优化的收敛时间，也不易于陷入局部最优解。我们需要根据具体的问题进行分析，如果根据我们的经验判断出最优解一定在某个范围内，则就在这个范围内初始化粒子。如果无法确定，则以粒子的取值边界作为初始化范围。

参考文献

粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读 - 知乎 (zhihu.com)

Matlab粒子群算法（PSO）优化程序——经典实例_matlab粒子群算法(pso)优化程序-CSDN博客