压缩感知主要应用于图像处理等领域，但是如果我们利用其特性，它在物理网领域也是可以得到较好的运用的，这篇博客主要是讲一种Compressive Data Gathering（CDG）方法在物联网数据收集中的应用。

采用压缩感知的优势

在物联网传输信息的过程中，我们单独抽出一条链路传输信息的过程来看.

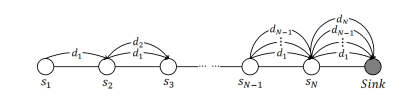
我们可以看到，在数据向Sink节点传输的过程中，单对传输这个过程来说，他的复杂度是$O(n^2)$的，同时，在传输的过程中，整个能量的消耗是不均匀的，越接近Sink节点的子节点能量消耗越大，这对于整个无线传感器网络的效率与维护是不利的，所以我们采用压缩感知算法来优化这一过程。

如何采用压缩感知算法

如下图所示：

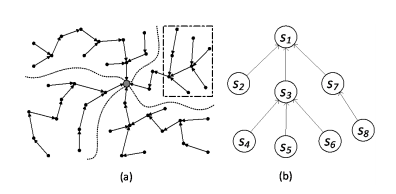
图a是一个常见的无线传感器网络，可以看到图中的Sink节点有四个子树（用虚线划分），我们取出其中一个子树作为样例来解释如何进行压缩，我们假设对节点$S_i$收集到的数据标记为$x_i$,那么根据压缩感知的理论我们就可以得到这样一个压缩的结果，如果对压缩感知没有概念的同学可以去看看我的上一篇文章：压缩感知基本概念

$y_i=\sum_{j=1}^N\phi_{ij}x_j$

对应到矩阵运算中就是

$\begin{Bmatrix} y_1\\ y_2\\ \vdots\\ y_M \end{Bmatrix} = \begin{Bmatrix} \phi_{11} &\phi_{12} &... &\phi_{1N}\\ \phi_{21} &\phi_{22} &... &\phi_{2N}\\ \vdots &&\vdots\\ \phi_{M1} &\phi_{M2} &... &\phi_{MN} \end{Bmatrix} \begin{Bmatrix} x_1\\ x_2\\ \vdots\\ x_M \end{Bmatrix}$

于是乎，我们的数据收集就由原来的$O(N^2)$复杂度变为现在的$O(NM)$复杂度，如下图

在上图中我们看到，每个数据点的传输从原来的1，2，3，4…，N个数据到现在的每个都是M个数据，不光降低了复杂度，同时也使得在整个传输过程中能量的均匀分布。

数据还原

OK，下面就是这篇文章的重中之重了，如何进行数据的还原，毕竟你也不想数据还原以后误差很大吧。

数据的稀疏化

这个在我上一篇文章中讲过，这里简单复述下。

由于压缩感知只有在对于稀疏信号的情况下才可以完整地还原信号，所以我们的想法就是找到一种变换方式使得在以下公式中我们得到的s是一个稀疏矩阵

$x_i=\sum_{j=1}^N\psi_{ij} s_j$

而在这篇文章中，作者采用的是离散余弦转换（DCT），但是这种转换只有部分情况才会产生离散情况，具体怎么产生，后面会讲。

当然，还有一个问题就是我们应该怎么确定M的取值呢，这里作者直接给出了一个公式

$M\geq c \cdot \mu^2(\Phi ,\Psi)\cdot K\cdot log N$

其中

$\mu(\Phi, \Psi)=\sqrt{N} \cdot \mathop{\max}_{1\leq i,j\leq N} | \langle \phi_i,\psi_j \rangle |$

通过计算我们可以大体得出M在3K~4K左右通常就可以满足我们的还原需求。

具体的还原算法

我看了下原文的方法和常见的还原算法差不多，就直接看我整理的这篇吧：常见还原算法

异常值的处理

原文的意思是这样的，如下图

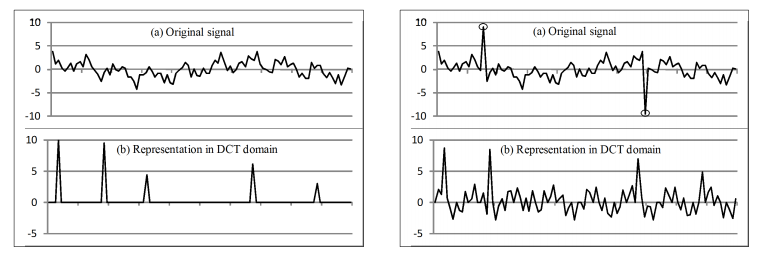
左图是正常情况下的信号以及其在DCT变换后的图像，右图是存在两个异常读数（两个圈出来的值）的情况下的DCT变换后的图像，可以看到右图存在异常读入的情况下DCT变换后的值明显是非稀疏，所以作者采用了一些方法来规避掉这种情况。

首先我们将我们的数据分解为两个部分

$x=x_0+x_s$

其中$x_0$为在某一变换域中的稀疏读数，$x_s$为异常读书的偏差值，由于异常读数是零星的，所以$x_s$在时域上是一个稀疏信号

那么根据之前我们得到的性质，我们可以得到：

$x=\Psi s_0+I s_s$

其中$I$为单位矩阵。这时我们得到的两个向量$s_0,s_s$都是稀疏的，也就是说我们将原信号分解成了两个不同域中的稀疏信号，这时候我们定义一个完备基：$\Psi ’ =[\Psi I]$，那么我们的原始信号就可以表示为(其实就是简单的线性代数)：

$x=\Psi' s,s=[s_0^T s_s^T]^T$

然后我们就把这个值丢到我们的还原算法里就好啦！

其实我觉得作者的这种做法是有点问题的，但是我没有仔细研究过DCT变换或者小波变换，也没法说他这里有啥问题，反正我在仿真的时候在一些情况下没有异常值的时候DCT变换也是会出问题的，这里挖个坑吧，研究下这些变换后看看是怎么个事，说不定就是一篇文章了（

大规模无线传感器网络压缩数据采集