压缩感知基本概念
奈奎斯特采样定理
想要让采样之后的数字信号完整保留信号中的信息,采样频率必须大于信号中最高频率的两倍!
为什么?
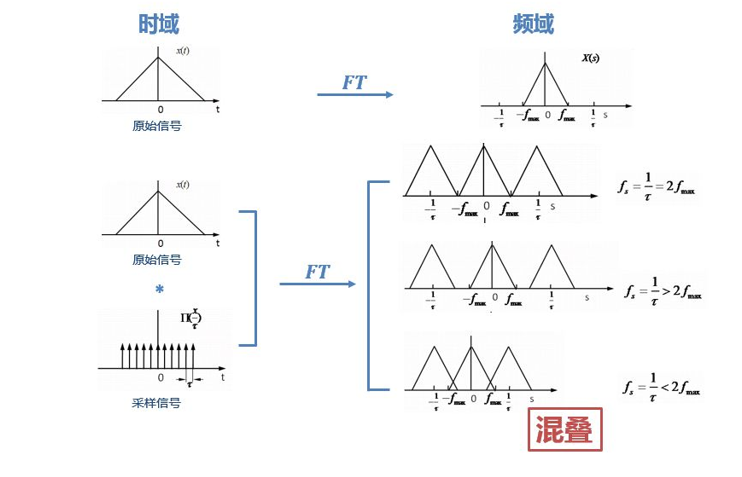
从下面这张图中可以看到,如果采样率比信号频率的两倍要低,那么在频域中信号会混叠,这个信号就和时域信号中的信号不一样了。
举个例子,对于一个$sin(2\pi x)$的信号,他的周期是$1$,频率就是$1$
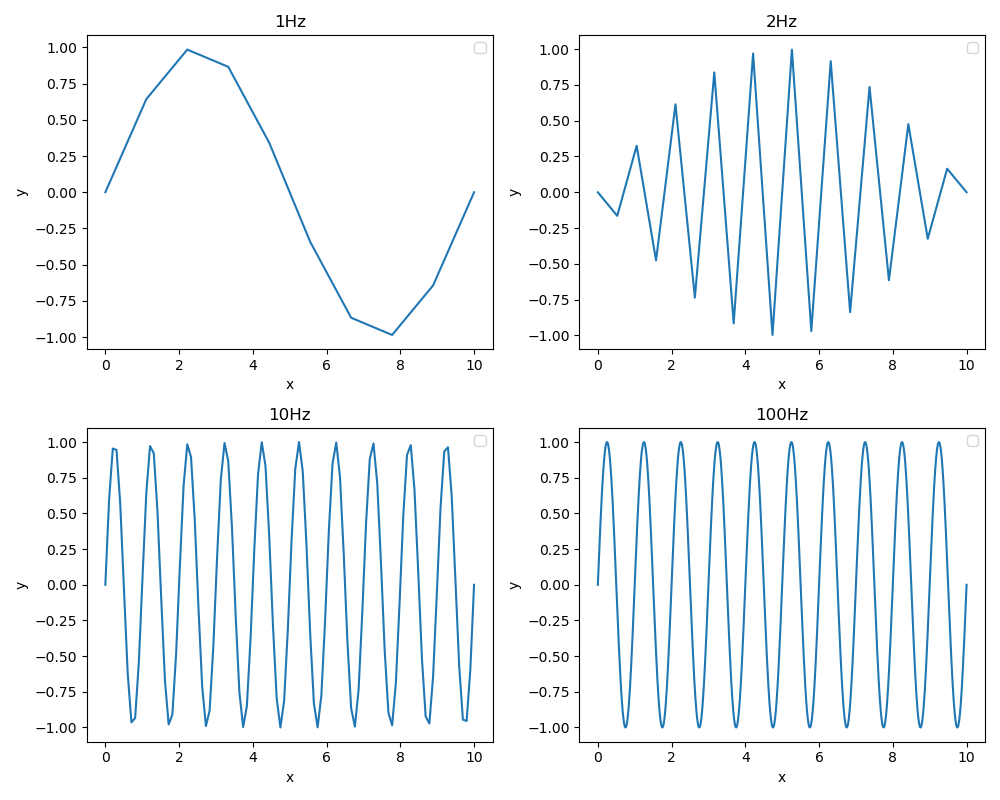
我们可以看到在1Hz的采样频率的情况下,图像已经和我们的原函数相差很大了,当2Hz的采样频率下才有点像了,当10Hz就已经十分甚至九分地像了。当然这是对于一个比较标准的三角函数来进行的模拟,感兴趣的读者可以试着自己做一下多个不同周期的正弦波叠加的信号在不同采样频率下的结果。
概念的提出
所以说我们可以粗略地得出一个结论,采样的频率越高,还原出来的原始信号就越符合原始信号!
但是,问题来了,我们一定要在那么高的采样率下进行数据收集嘛?很显然,这是一种资源的浪费,所以,在2004年,三位大牛证明出,如果信号是稀疏的,那么它就可以由远低于上述采样定理要求的采样点重构恢复,并于2007年正式提出了“压缩感知”

为什么
在奈奎斯特采样理论中,我们使用的是采样频率,这就意味着我们进行的是等间距采样,而这样就会使得我们获得的信号在频域中以$\frac{1}{\tau}$为周期延拓,这就导致了混叠。
那我们应该如何规避掉这个问题呢,首先根据上文我们可以知道,混叠的根本原因就是等间距采样,所以,只有改变采样方式,我们才可以打破这个限制,于是乎,我们就需要进行随机采样。这样说可能有点含糊,给你们看两张图。
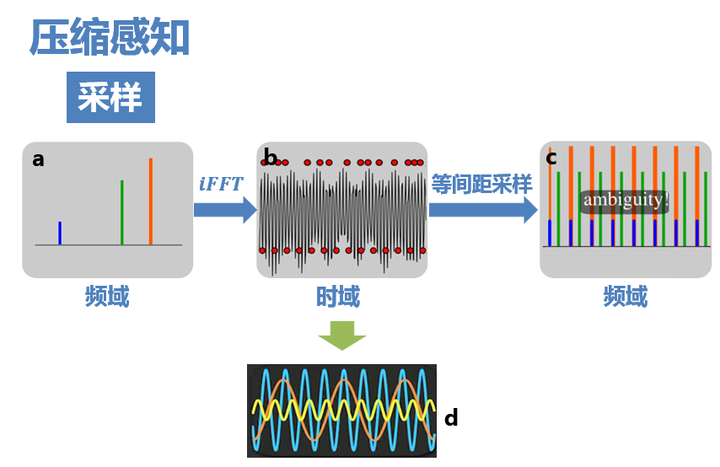
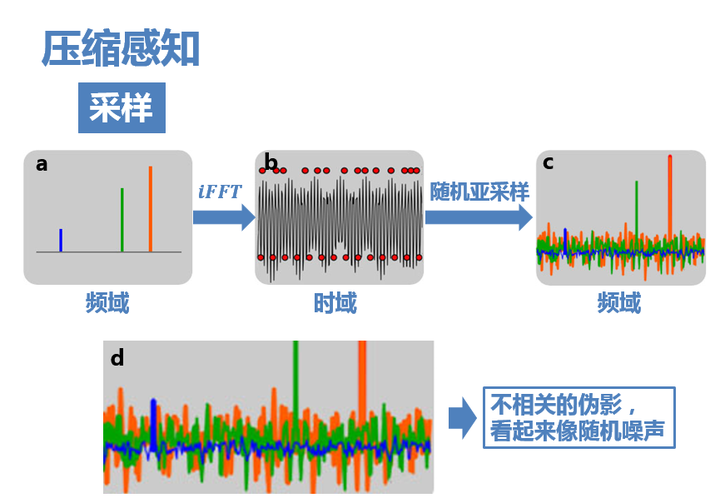
第一张图中采用下方的等间距采样,我们可以发现,由于频域信号周期延拓,我们的信号产生了混叠吗,而且是有规律有周期的混叠,那么我们从中恢复出原始信号的可能性是0。但是我们看第二张图,它是采用上方的上随机亚采样,虽然还是存在信号延拓,但是他不是有规律的,有周期的,它产生了大量不相关(注意,这个在后面很有用)的干扰值,但是呢,在图c中,我们原始信号的那几个峰值依稀可见,只是一定程度地被干扰值覆盖了,所以,根据这个特性,我们可以来重构我们原始信号了。
怎么还原(形象化地表示)
经典算法:匹配追踪
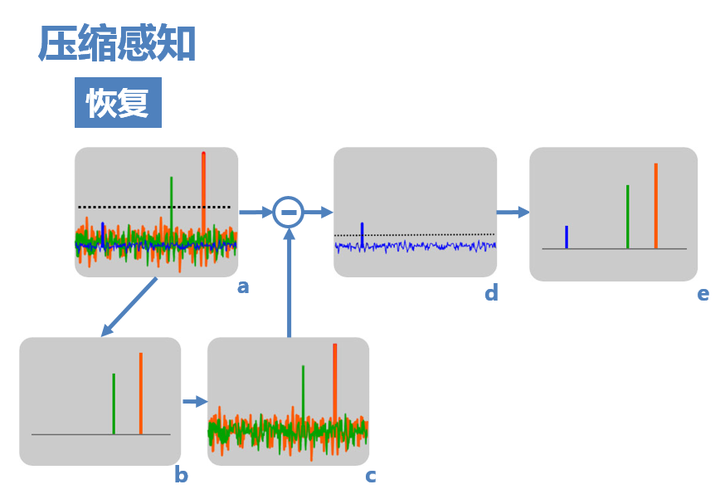
由于原信号的频域中非零值在采样过后的频域中任然保留了较大的值,那么其中部分节点,如图a中的的黄绿两个值,可以通过设置阈值来得到,具体流程就是图a->图b->图c。
有部分信号可能需要通过它单独的非零值和其自身产生的干扰值实现还原,也是通过设置阈值来实现,如图d。
小结论
所以,到这里,我们就可以得到压缩感知理论的核心思想——以比奈奎斯特采样频率要求的采样密度更稀疏的密度对信号进行随机亚采样,由于频谱是均匀泄露的,而不是整体延拓的,因此可以通过特别的追踪方法将原信号恢复。
前提条件
大前提
通过上面的例子,我们可以知道想要实现信号的恢复,在采样过程中必须保证两个大前提:
- 信号在频域中稀疏
- 采用随机亚采样,使得频率泄露均匀分布在频域中。
如何实现
在某个域中只有少量非零值,则称之为稀疏,具体来说就是非零点远远小于信号总点数。
一、如何稀疏?
那么问题来了,我们应该如果使得我们采集的信号是稀疏的呢?这就需要一点点数学知识了。
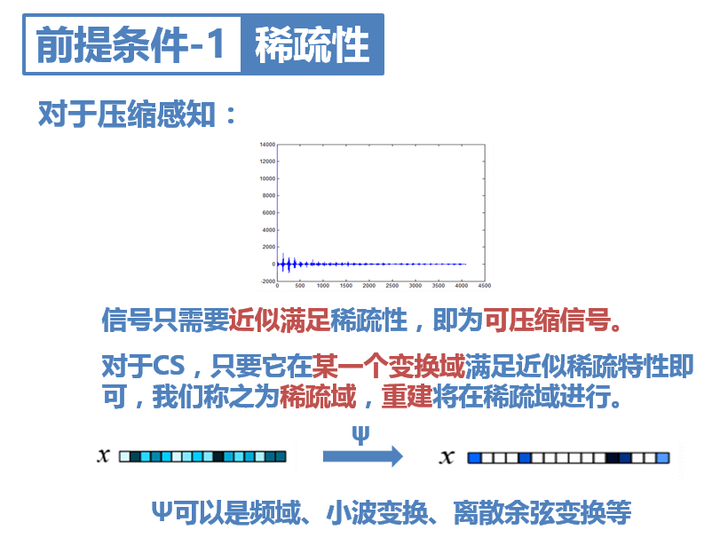
学过傅里叶变换的同学可能知道,任何函数都可以表示为n个正弦波和余弦波叠加得到(没学过的同学可以去百度,了解下基本概念就好了),这样我们就将时域信号转化为了频域信号,但是显然,傅里叶变化得到的大部分频域信号都是非稀疏的。
所以我们可以通过别的方法将时域信号转换到某个特定域,从而实现信号的稀疏化,常见的就是小波变换,离散余弦变换(DCT)这些。
数学表达
说到这里,我们之前得到的结论都可以通过数学方式来得到。具体如下图所示。
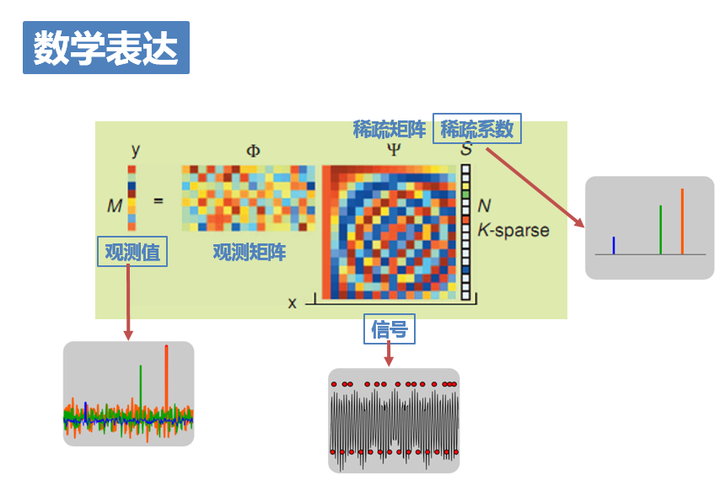
其中$\Phi$为观测矩阵,就是我们压缩的数据,将高维数据压缩至低维数据的重点,通过矩阵乘法将n维的矩阵转换为m维的矩阵,其实就是一个投影的过程。
而之前提到我们需要对原始信号进行稀疏化,那怎么进行稀疏化呢?我们来看这张图中的$x$,它是通过$n\times n$的矩阵$\Psi$和$n\times 1$的矩阵s相乘的到,其中,x表示的是一个一维的原始信号,而$\Psi$则是我们上面说的对信号进行稀疏化操作的一个变换矩阵,而s则是我们得到的稀疏矩阵。
所以对原始信号的稀疏化我们就可以表示为$x=\Psi s$,相关数据的定义已在上一段给出。
所以总的流程就是$y=\Phi \Psi s$,其中$\Psi s$表示原始信号,s为原始信号的稀疏表达。
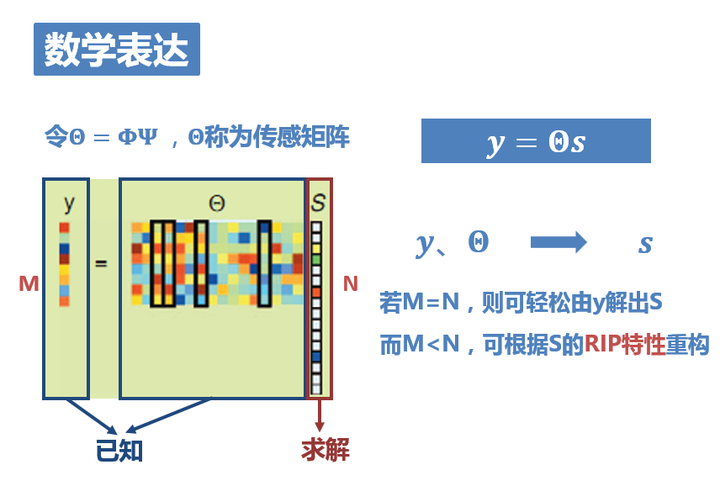
所以说,现在的问题就比较简单明了了,由于原公式有点长,我们令$\theta =\Phi \Psi$,在还原过程中,我们就只需要关注一个问题:在$y=\theta s$的情况下,y和$\theta$已知,如何求解s,这个放到文章后面来讲。
二、不相关性
前面我们提过我们需要使用随机亚采样才能实现我们需要的我们的目的,这就说明我们需要通过证明观测矩阵和稀疏表示基之间相关性很低才行,换句话来说就是$\Phi \Psi $不相关。具体证明可以看图了解一下。、


观测矩阵$\Phi $的选取
一般来说,我们都是采用高斯矩阵,这个矩阵已经可以做到很好的效果了。
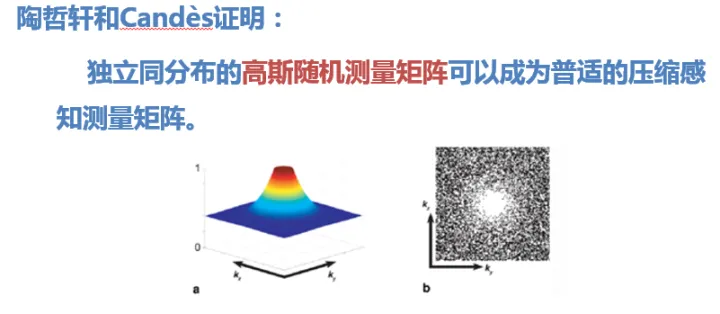
当然,如果你有别的办法来构建观测矩阵的话,请联系我带我上一区TOP,谢谢!
那么问题来了,有啥用?
举个简单的例子,核磁共振的时候,采样时很慢的,你也不希望一直暴露在辐射里面吧,那么我们就可以通过压缩感知的方法来快速出图,还有比如在大规模无线网络中的应用,或者说在联邦学习等之中,都可以使用压缩感知进行优化。
参考文献:
